备注

  • 语法为 ES6
  • 以下排序默认按升序排序
  • 测试案例均为自然数

前言

排序作为十分经典的算法之一。是每一个软件工程师的必备技能，学好排序算法，可以提高软件的运行效率，最重要的是掌握其算法设计思想，才能举一反三应用到实际的实践中，为己所用。

排序算法简介

  1. 按照数据的大小，排序算法可以分为内部排序和外部排序（数据较大，需要借助外存）
  2. 内部排序，又可以细分为 交换排序、插入排序、选择排序

1. 冒泡排序

简介：两两元素进行比较，较大者放置后头，类似水中的气泡较大者浮在水的上端

性能

平均时间复杂度 O(n^2)

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
function bubble(arr) {
    let len = arr.length,
        i = 0,
        j = 0;
    // 循环 n-1 趟
    for (i = 0; i < len; i++) {
        // 每趟 需比较 n-i-1 次
        for (j = 0; j < len - 1 - i; j++) {
            // 如果后面的元素较大，则交换两者顺序
            if (arr[j + 1] < arr[j]) {
                arr[j] = [arr[j + 1], arr[j + 1] = arr[j]][0];
            }
        }
    }
    return arr;
}

2. 快速排序

简介：取一个元素为基准，把序列分成两部分，小于基准的放到它的左面，大于等于的放到它的右面，然后在把左面和右面的子序列再进行上述的拆分，直到子序列不可再分割（小于2个元素），最终达到整个序列有序

性能

平均时间复杂度 O(n*logn)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
function quick(arr) {
    // 不可再分割，直接退出
    if (arr.length <= 1) return arr;
    let len = arr.length,
        middle = len >> 1,
        pivot = (len--) && arr.splice(middle, 1)[0], // 取中间为基准数，并从数组中移除
        left = [],
        right = [],
        i = 0;

    for (i = 0; i < len; i++) {
        // 分组 小于基准的放到左边，反之
        if (arr[i] < pivot) {
            left.push(arr[i]);
        } else {
            right.push(arr[i]);
        }
    }
    return [...quick(left), pivot, ...quick(right)]; // 合并
}

3. 简单选择排序

简介：假设一个有序序列，然后由剩余的元素中选出最小的（最大的）扔到有序序列，直到无序序列元素为空，从而达到整个序列有序

性能

平均时间复杂度 O(n^2)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function selection(arr) {
    let len = arr.length,
        i = 0,
        j = 0,
        min = i;
    // 循环 n-1 趟
    for (i = 0; i < len - 1; i++) {
        min = i; // 假设每趟的第一个数为最小值
        for (j = i + 1; j < len; j++) {
            // 如果后面的树大于最小数（min对应的数），则重新对最小值的索引赋值
            if (arr[j] < arr[min]) {
                min = j;
            }
        }
        // 将最小数置于该趟排序的第一个位置
        arr[i] = [arr[min], arr[min] = arr[i]][0];
    }
    return arr;
}

4. 堆排序

简介：是简单选择排序的改进版，利用堆结构

性能

平均时间复杂度 O(n*logn)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 堆排序
function heapSort(arr) {
    var n = arr.length,
        i, j;

    // 筛选
    var sift = (k, m, r) => {
        var p = k, // 父结点
            c = p * 2 + 1; // 左结点（默认最大）

        while (c <= m) { // 左结点(c=m)和左右结点(c<m)
            if (c < m && r[c + 1] > r[c]) c++; // 选出左右结点中的最大者，指向左结点
            if (r[p] > r[c]) break; // 父结点大于左结点 顺序正确，退出循环
            else {
                r[p] = [r[c], r[c] = r[p]][0]; // 将大的一方置于顶部（父结点）
                p = c; // 向下重新指向父结点
                c = p * 2 + 1; // 向下重新指向左结点
            }
        }
    };

    // 构建堆
    for (i = (n / 2 | 0) - 1; i >= 0; i--) { // 从最后一个分支结点开始向上逆序遍历 
        sift(i, n - 1, arr);
    }
    // 排序
    for (j = n - 1; j >= 0; j--) {
        arr[0] = [arr[j], arr[j] = arr[0]][0]; // 将最大的结点存于数组的最后一位
        n--; // 减少数组长度，排除有序序列
        sift(0, n - 1, arr, true);
    }

    return arr;
}

5. 直接插入排序

简介：假设数组的一有序序列，从后面的无序序列中，扫描，与有序序列比较，插入到合适位置

性能

平均时间复杂度 O(n^2)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
function insertion(arr) {
    let len = arr.length,
        i = 0,
        j = 0,
        temp;

    // [7,6,2,5,4,3,1]
    // 从第二个元素开始循环
    for (i = 1; i < len; i++) {
        temp = arr[i]; // 存储当前元素
        j = i - 1; // 待插入队列的序号
        while (j >= 0 && temp < arr[j]) { // 当没有出界 且 当前元素比待插序列元素小时，进行待插序列的元素向后移动一位
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = temp; // 将当前元素插入到待插序列的下一位
    }
    return arr;
}

6. 希尔排序

简介：一种改进版的插入排序，每次比较的是用增量分割的序列，达到部分有序，随着增量依次递减，序列逐渐达到完全有序

性能

平均时间复杂度 O(n*logn)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
function shell(arr) {
    let len = arr.length,
        i = 0,
        j = 0,
        temp,
        gap = 1;
    
    gap = len / 3 | 0; // 计算增量

    while (gap >= 1) { // 增量大于2时，进行简单插入排序
        for (i = gap; i < len; i++) {
            temp = arr[i];
            j = i - gap;
            while (j >= 0 && temp < arr[j]) {
                arr[j + gap] = arr[j];
                j -= gap;
            }
            arr[j + gap] = temp;
        }
        gap = gap / 3 | 0; // 增量减少
    }

    return arr;
}

7. 归并排序

简介：利用分治法，将序列分为许多小子序列，然后每个子序列进行排序，然后逐次合并，最后达到整体有序，这里用的是二路归并排序（归并排序中最简单的一种）

性能

平均时间复杂度 O(n*logn)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
function merge(arr) {
    return ({
        sortArr(leftArr, rightArr) { // 排序
            let res = [];
            // 合并
            while (leftArr.length * rightArr.length !== 0) {
                if (leftArr[0] < rightArr[0]) {
                    res.push(leftArr.shift());
                } else {
                    res.push(rightArr.shift());
                }
            }
            leftArr.length > 0 && (res = [...res, ...leftArr]);
            rightArr.length > 0 && (res = [...res, ...rightArr]);
            return res;
        },
        mergeArr(brr) { // 合并
            if (brr.length <= 1) return brr;
            let len = brr.length,
                left = [],
                right = [],
                middle;
            middle = len >> 1;
            // 分组
            left = brr.slice(0, middle);
            right = brr.slice(middle);
            return this.sortArr(this.mergeArr(left), this.mergeArr(right));
        }
    }).mergeArr(arr)
}

8. 计数排序

简介：利用分配概念，将元素一一映射到桶中，每个桶只存储单一值

性能

平均时间复杂度 O(n+m)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function countingSort(arr) {
    var max = Math.max(...arr),
        min = Math.min(...arr),
        len = arr.length,
        i,
        bucket = [],
        result = [];

    // 入桶
    for (i = 0; i < len; i++) {
        var item = arr[i];
        bucket[item] = bucket[item] || 0; // 建立映射表
        bucket[item]++; // 相同元素对应到同一映射表中，映射表增加1 
    }

    // 出桶
    for (i = min; i <= max; i++) {
        var count = bucket[i]; // 取每个映射表的元素数量
        while (count > 0) { // 如果数量大于0 ，重复输出该元素 
            result.push(i);
            count--;
        }
    }

    return result;
}

9. 桶排序

简介：利用分配概念，每个桶存储一定范围的数值，然后桶内在进行排序，最后所有桶的元素出桶达到完全有序

性能

平均时间复杂度 O(n+m)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
function bucketSort(arr, num) {
    var len = arr.length,
        max = Math.max(...arr),
        min = Math.min(...arr),
        result = [],
        bucket = [],
        space,
        i;
    // 至少2个桶
    num = num > 2 ? num : 2;
    // 计算每个桶的容量
    space = ((max - min) / num | 0) + 1;

    // 入桶
    for (i = 0; i < len; i++) {
        var item = arr[i];
        var index = (item - min) / space | 0; // 计算元素入桶的位置，要放入哪个桶

        bucket[index] = bucket[index] || [];
        bucket[index].push(item);
        if (bucket[index].length > 1) {
            // 桶里的元素再进行排序（这里使用的是简单插入排序）
            bucket[index] = insertion(bucket[index]);
        }
    }

    // 出桶
    for (i = 0; i < num; i++) {
        var list = bucket[i] || [];
        if (list.length > 0) {
            result = result.concat(list);
        }
    }

    return result;
}

10. 基数排序

简介：利用分配概念，根据元素的基数来分配桶

  • 最低位优先法，简称LSD法：先从最低位开始排序，再对次低位排序，直到对最高位排序后得到一个有序序列

  • 最高位优先法，简称MSD法：先从最高位开始排序，再逐个对各分组按次高位进行子排序，循环直到最低位

性能

平均时间复杂度 O(n*m)

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
function radixSort(arr) {
    var len = arr.length,
        max = Math.max(...arr),
        bucket = [],
        result = [],
        i,
        j,
        k,
        hight = String(max).length; // 计算最大数的位数

    for (i = 1; i <= hight; i++) { // 其实就是循环hight次的计数排序
        result = [];
        bucket = [];
        // 入桶
        for (j = 0; j < len; j++) {
            var item = arr[j] + ""; // 这里转换为string 类型，方便取具体位数的值，当然mod10也可以
            var index = item.length - i < 0 ? 0 : item.substr(item.length - i, 1); // 取第(item.len-i+1)位的数
            bucket[index] = bucket[index] || []; // 这里就和计数排序一样了
            bucket[index].push(+item);
        }
        // 出桶
        for (k = 0; k < bucket.length; k++) { 
            if (bucket[k] && bucket[k].length > 0) {
                result = result.concat(bucket[k]);
            }
        }

        arr = result;
    }

    return result;
}

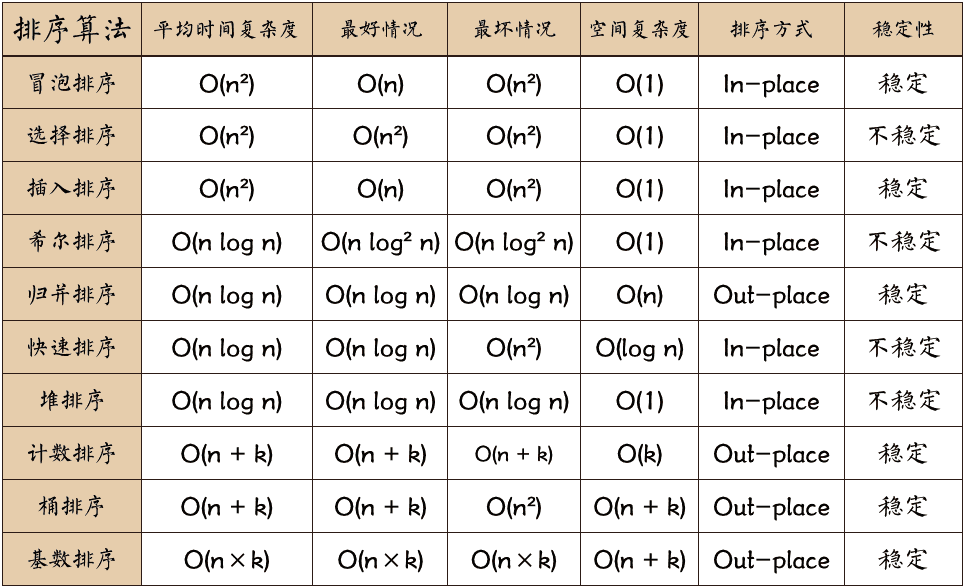
性能比较

sort
sort

参考

  1. 《十大经典排序算法》